What is Topological Sort?

It is a sorting algorithm that sorts the vertecis of a Directed Acyclic Graph (DAG) such that for every directed edge u - v, u comes before v. Sounds confusing? Let me make it simple. Just take the following simple graph with three vertex:

U -> V -> W

Now if I write it in topological sort it would be:

U, V, W

Here you can see U comes before V and V comes before W.

Lets take another graph:

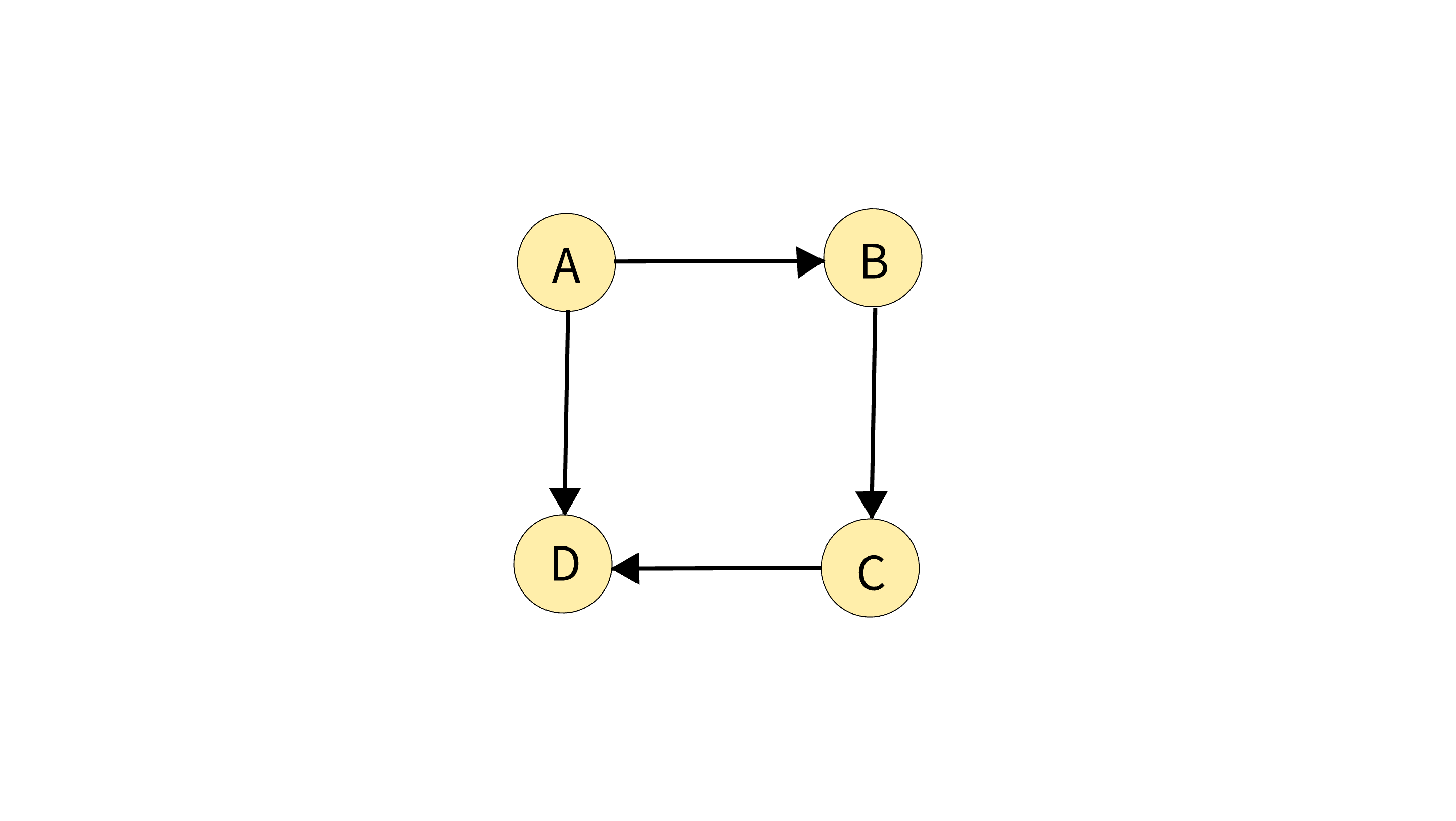
Here the topological sort can be:

A, B, C, D

But if we write

A, D, B, C

It will be wrong since D came before C which should not happen.

Real world use:

One of the real world use is say you are scheduling some tasks which should be done in order and dependent on each other in some way. Take the above examle itself. I am gonna make it more relatable, Imagine a system that generates recomendations for users in a shopping website. We can devide the work into multiple tasks and make a graph which is same as the above graph. Following are the tasks assigned to each of the vertex:

A: Fetch data from user database(email, gender) who lives in "Assam".
B: Fetch data from shopping database of purchase history (email, item, price) and map them with data from A.
C: Take the data from B and train a Recomendation system 
D: Take the ML model generated by C and the users data from A to produce a dataset which has (email, recomended_item).

Now you can see, the tasks are dependent on previous tasks. Without them they can not perform themselves. D can not do it's task unless A and C finishes. So A and C must come before D. Similarly B should come before C but after A.

Note: Depending on the graph, there can be more than one topological sorting order

Implimentaion

To implement Topological sort, we can simply perform Depth First Search (DFS) and take help of Stack data structure. So what we will do is we will perfrom depth first search and when it completes visiting all the vertices of the graph we will put the elements to a stack while backtracking. Here staring from A, performing DFS in forward will be

A(visited) -> B(visited)-> C(visited) -> D(visited)

Now in Backtracking part of DFS,

1. A(visited) -> B(visited)-> C(visited) <- D(push to stack)
2.  A(visited) -> B(visited)-> C(push to stack) <- D(push to stack)
3.  A(visited) -> B(push to stack)<- C(push to stack) <- D(push to stack)
4. A(push to stack) <- B(push to stack)<- C(push to stack) <- D(push to stack)

so at this point of time the stack will be:

						    | A | <- top
						    | B |
						    | C |
						    | D |
						    -----

We will pop the stack and inset it to a list which is going to be the Topological ordered list

					    [A, B, C, D]

Java Implementation:

We will create some classes to better organize and scale our code.

DirectedEdge.java

public class DirectedEdge{
    private final int start;
    private final int end;
    private final float weight;

    public DirectedEdge(int start, int end, float weight){
        this.start = start;
        this.end = end;
        this.weight = weight;
    }
    public int from(){
        return this.start;
    }
    public int to(){
        return this.end;
    }
    public float getWeight(){
        return this.weight;
    }
    public String toString(){
        return start + "-"  +"->" + end;
    }
}

EdgeWeightedDiagraph.java

import java.util.ArrayList;
import java.util.List;
import java.util.stream.Collector;
import java.util.stream.Collectors;
import java.util.stream.IntStream;

public class EdgeWeightedDiagraph {


    private final int V;
    private final ArrayList<ArrayList<DirectedEdge>> adjList;

    public EdgeWeightedDiagraph(int V){
        this.V = V;
        this.adjList = new ArrayList<>();

        for(int i  = 0; i < V; i++){
            this.adjList.add(i, new ArrayList<>()); 
        }
    }
    public int numVertices(){
        return this.V;
    }

    public void addEdge(DirectedEdge edge){
        int v = edge.from();
        this.adjList.get(v).add(edge);
    }
    public Iterable<DirectedEdge> getAdjListOfVertex(int v){
        return this.adjList.get(v);
    }
    public Iterable<Integer> getVertices(){
        return IntStream.range(0, adjList.size()).boxed().collect(Collectors.toList());
    }
    public void removedEdge(DirectedEdge edge){
        int i = 0;
        for(DirectedEdge e: this.getAdjListOfVertex(from)){
            if(e.to() == edge.to() && e.from() == edge.from() && e.getWeight() == edge.getWeight()){
                break;
            }
            i++;
        }
        this.adjList.get(from).remove(i);
    }
}

Callback.java

public interface Callback<T> {
    void  call(T  result);
}

TopologicalSort.java

import java.util.Stack;

public class TopologicalSort {
    private EdgeWeightedDiagraph graph;
    private Integer[] vertices;

    public TopologicalSort(EdgeWeightedDiagraph graph, Integer source){
        vertices = new Integer[graph.numVertices()];
        Stack<Integer> stack = new Stack<>();

        Callback<Integer> callback = new Callback<Integer>() {
            @Override
            public void call(Integer result) {
                stack.push(result);
            };
        };
        DFS dfs = new DFS(graph, source, callback, true);
        int i = 0;
        while(!stack.empty()){
            vertices[i++] = stack.pop();
        }
    }

    public Integer[] getSortedVertices(){
        return this.vertices;
    }
    public static void main(String[] args) {
        EdgeWeightedDiagraph graph = new EdgeWeightedDiagraph(4);
        graph.addEdge(new DirectedEdge(0, 1, 0));
        graph.addEdge(new DirectedEdge(0, 2, 0));
        graph.addEdge(new DirectedEdge(1, 3, 0));

        TopologicalSort topologicalSort = new TopologicalSort(graph, 0);

        for(int i = 0; i < topologicalSort.getSortedVertices().length; i++){
            System.out.println(topologicalSort.getSortedVertices()[i]);
        }
    }
}